问题现象

某客户将其应用从某UNIX平台移植到AIX后，在做原平台和 AIX 批量比对时发现，定期自动转存后， AIX 有 数千用户结息金额比原平台少一分钱，原因都是小数点后第三位是 5 时没有正常进位。分析后发现是底层的四舍五入函数，在 原平台上运行没有问题，在 AIX 上对部分小数点后第三位为 5 的金额能进位，部分就进不了位。
用户希望确认两个系统的数字精度是不是确实有上述差异。谢谢！

分析结论

对出错的账户结息数值进行分析发现，这种精度问题属于计算平台二进制浮点表示（请参阅IEEE 754标准）的固有瓶颈，需要采用修正策略进行一定程度的规避；或者考虑使用 POWER 架构的十进制浮点数来进行运算，从根本上解决问题。详细情况如下：

根本问题是，二进制浮点数（默认的计算机存储格式）无法准确地表示十进制浮点数，比如：

十进制 0.735 ，在二进制表示下是无限循环小数，按 64 位 binary double 存储就会引入四舍五入误差。将二进制存储的 0.735 使用十进制表示就变成了： 0.73499999999999998667732370449812151491641998291015625...

在误差值不大时，可以通过增加一个固定的 delta 来进行修正，比如客户目前采用的加上 1.0e-15 的方式。

但是，需要注意的是，所谓64bit double的 15~17 位十进制数值精度是包含十进制形式的整数部分和小数部分的；按浮点表示法，浮点数存储时都会被泛化成相同的格式，即 1.xxxxx (2*exponent), 参考：

https://en.wikipedia.org/wiki/Double-precision_floating-point_format

...

The IEEE 754 standard specifies a binary64 as having:

· Sign bit: 1 bit

· Exponent width: 11 bits

· Significand precision: 53 bits (52 explicitly stored)

This gives 15 – 17 significant decimal digits precision.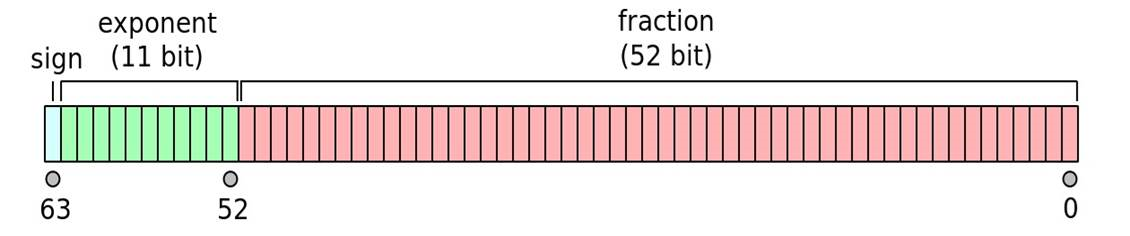

当数值足够大，且超出 15 位十进制精度时，增加 delta 的方法就不一定能凑效，比如 128.015 ，在 64 位 double 和 128 位 long double 的表示分别是：

128.0149999999999863575794734060764313000000 <= 64bit double

128.0149999999999999999999999999994951000000 <= 128bit double

这种情况下，加 1.0e-15 的修正方式对 long double(128 位 ) 有效，但对普通的 double 类型（ 64 位）无效。

示例代码以及运行结果如下：

#cat double1.c
#include <stdio.h>
#include <stdlib.h>
#include <math.h>

int main(){

long double bb;

double aa;

double dOffset;

int iDec = 2;

aa=128.015;

bb=128.015L;

printf("a=%.40lf\\n",aa);

printf("b=%.40Lf\\n",bb);

printf("a=%.2lf\\n",aa);

printf("b=%.2Lf\\n",bb);

aa += ( dOffset = 1.00 / pow (10.0, (double)(iDec + 13)) );

bb += ( dOffset = 1.00 / pow (10.0, (double)(iDec + 13)) );

printf("epsilon = %.40Lf\\n",dOffset);

printf("a+epsilon=%.40lf\\n",aa);

printf("b+epsilon=%.40Lf\\n",bb);

printf("a+epsilon=%.2lf\\n",aa);

printf("b+epsilon=%.2Lf\\n",bb);

printf("a+16epsilon=%.40lf\\n",aa + 15.0*dOffset);

return 0;

}

#xlc128 double1.c -q64 -o double1 -lm

#./double1

a=128.0149999999999863575794734060764313000000 <= 64 位 double 取值

b=128.0149999999999999999999999999994951000000 <= 128 位 double 取值

a=128.01

b=128.01

epsilon = 0.0000000000000010000000000000000777053999

a+epsilon=128.0149999999999863575794734060764313000000 <= 64 位 double 下，加上 1e-15 的修正之后的效果（ **无效** ）；

b+epsilon=128.0150000000000009999999999999983895000000 <= 128 位 double 下，加上 1e-15 的修正之后的效果（**有效**）；

a+epsilon=128.01

b+epsilon=128.02

a+16epsilon=128.0150000000000147792889038100838661000000 <= 64 位 double 下，加上 16*1e-15 的修正之后的效果（ **有效** ）；

综上，临时解决方法可以有如下选择：

1. 提高 delta 的取值，从 1.0e-15 提高到例如 1.0e-10 或更大的数值等等 ;

   需要对代码的 delta 取值做修改；

2. 采用 long double （ 128 位精度）取代 double （ 64 位精度）；

   需要对代码中的数据类型进行修改，并且同时采用 xlc128/xlc128_r 编译（说明 : 如果是使用多线程的应用，需要采用 _r 后缀的编译命令）。

如果需要彻底的解决方法，建议采用硬件级十进制浮点功能 ，示例代码如下：

#cat decimal.c

#include  <stdlib.h> 
#include  <math.h> 

int main(){

_Decimal128 bb;

_Decimal64 aa;

_Decimal64 dOffset;

int iDec = 2;

aa=128.015DD;

bb=128.015DL;

printf("a=%.40Df\\n",aa);

printf("b=%.40DDf\\n",bb);

printf("a=%.2Df\\n",aa);

printf("b=%.2DDf\\n",bb);

return 0;

}

#xlc -qdfp decimal.c -q64 -o decimal -lm -qarch=pwr7

注意为启用DFP功能，-qarch必须设置为pwr6或以上，比如-qarch=pwr7，-qarch=pwr8等等。

#./decimal

a=128.0150000000000000000000000000000000000000

b=128.0150000000000000000000000000000000000000

a=128.02

b=128.02

参考：

https://www.ibm.com/developerworks/community/wikis/home?lang=en#!/wiki/Power+Systems/page/POWER6+Decimal+Floating+Point+%28DFP%29

问题总结

如上述示例，十进制浮点数在传统二进制浮点计算方式下，存在固有的精度误差，不太适合支付、金融等商务计算领域，建议引入十进制浮点数（如上文示例_Decimal类型，Java BigDecimal，python的Decimal等等）。POWER芯片的原生十进制浮点计算功能可以提高商务领域浮点表示的准确性，并大大提高计算速度。